A Wordament Solver
Or how to search 12 million words
Introduction
When I was younger, I used to play a word game called Boggle, where one would try to find as many words as possible from random letters. I had always suspected that I wasn’t good at the game; luckily for me, Wordament, Microsoft’s online multiplayer tournament version, left me in no doubt at all.
Clearly, if I was to improve my score, I would need to diligently practice cheat.
Grid and Tiles
The game is simple; given 16 letter tiles, create as many words as possible, while:
- only using a tile once per word
- maintaining a continuous tile sequence

For example, RIOT is valid, but PILOT would not be allowed.
To represent the grid above, I decided on a simple implementation where a tile was an integer:
enum Grid : int {width=4, height=4, size=Grid.width*Grid.height}
alias Tile = int;
enum TileNA = -1;
enum Dir {up, down, left, right, upLeft, upRight, downLeft, downRight}
This would allow simple mathamatical checks on the tile itself to infer where in the grid it would be. Take a 4x4 grid that’s set out in the following way:
|0 |1 |2 |3 |
|4 |5 |6 |7 |
|8 |9 |10|11|
|12|13|14|15|
Any number less then the width of the grid is in the first row (and thus no up tile); any number equal to or greater than width *(height-1) will be the last row (and thus no down tile), and so on and so forth.
auto isFirstRow (Tile tile){
return (tile < Grid.width);
}
auto isLastRow (Tile tile) {
return (tile >= Grid.width*(Grid.height-1));
}
auto isFirstColumn (Tile tile) {
return (tile % Grid.width == 0);
}
auto isLastColumn (Tile tile) {
return (tile % Grid.width == Grid.width-1);
}
Once we can establish if a tile is not on a particular edge, it’s trival to obtain tile in a particular direction.
auto getTile (Tile tile, Dir dir) {
if (tile==TileNA) return TileNA;
final switch (dir) {
case Dir.up: return (tile.isFirstRow) ? TileNA : tile - Grid.width;
case Dir.down: return (tile.isLastRow) ? TileNA : tile + Grid.width;
case Dir.left: return (tile.isFirstColumn) ? TileNA : tile - 1;
case Dir.right: return (tile.isLastColumn) ? TileNA : tile + 1;
case Dir.upLeft: return tile.getTile(Dir.up).getTile(Dir.left);
case Dir.upRight: return tile.getTile(Dir.up).getTile(Dir.right);
case Dir.downLeft: return tile.getTile(Dir.down).getTile(Dir.left);
case Dir.downRight: return tile.getTile(Dir.down).getTile(Dir.right);
}
}
unittest {
assert (0.getTile(Dir.right)==1);
assert (1.getTile(Dir.left)==0);
assert (5.getTile(Dir.downRight)==10);
assert (13.getTile(Dir.upLeft).getTile(Dir.right)==9);
}
TODO: need to limit unittest to only test 4x4 grid
Paths
The main logic of the program will be to work through every single sequence of tiles (or paths) possible, and check the words generated by the paths against a dictionary.
Given the millions of paths that a grid 4x4 or larger would generate, it makes sense to do as much pre-computing as possible; in this case, for each tile, I’ve created a mapping to its neighbouring tiles:
immutable Tile[][Tile] tileNeighbours;
static this() {
auto getNeighbours (Tile tile) {
import std.traits : EnumMembers;
Tile[] rvalue;
foreach (dir; EnumMembers!Dir) {
rvalue ~= tile.getTile (dir);
}
return rvalue.filter!(a => a != TileNA).array;
}
import std.typecons : tuple;
tileNeighbours = iota(0,Grid.size) // for each tile in our grid
.map!(a => tuple(a, getNeighbours(a))) // get all the tiles that surround it
.assocArray; // and store for fast reference
}
auto neighbours (Tile tile) {
return tileNeighbours[tile];
}
unittest {
assert (11.neighbours.dup.sort.equal([6,7,10,14,15]));
}
Now we can obtain the neigbouring tiles of any particular tile, we can recursively generate paths (a “tree traversal”). Take a 2x2 grid:
|0 |1 |
|2 |3 |
The tree representing all paths looks like:
Traversing these paths would get six 4-tile paths, six 3-tile paths, three 2-tile paths, and one 1-tile path - 16 paths in total. Did I say total? I meant total paths that start with tile 0. To get all paths, you also need to traverse the tree that starts with tile 1, the tree that starts with tile 2, and the tree that starts with tile 3. That will give 64 paths in total…total.
And here’s how we do it:
alias Path = Tile[Grid.size];
Path currentPath = TileNA.repeat(Grid.size).array; // initialise "null" path
auto currentIndex=0;
void traverse (Tile tile) {
// step forward, add tile to path
currentPath[currentIndex] = tile;
currentIndex++;
// look for next tile to add
foreach (n; tile.neighbours) {
if (!currentPath[].canFind(n)) traverse (n);
}
// ------
// path finished, do work with path
// ------
// step back, remove tile from path
currentIndex--;
currentPath[currentIndex] = TileNA;
}
iota(0,Grid.size).each!(a => traverse(a)); // for each tile, do a tree traversal
Using our same 2x2 grid, for tile 0 it would produce the paths:
[0, 2, 3, 1]
[0, 2, 3, -1]
[0, 2, 1, 3]
[0, 2, 1, -1]
[0, 2, -1, -1]
[0, 1, 3, 2]
[0, 1, 3, -1]
[0, 1, 2, 3]
[0, 1, 2, -1]
[0, 1, -1, -1]
[0, 3, 1, 2]
[0, 3, 1, -1]
[0, 3, 2, 1]
[0, 3, 2, -1]
[0, 3, -1, -1]
[0, -1, -1, -1]
Words
We have our paths (which for a 4x4 grid, is over 12 million). We now need our words. Two types of words, in fact.
Dictionary Words
In an ideal world, we would use the exact word list that the Wordament game itself uses, however, my Google-fu was not strong enough to obtain such a list, so I ended up trying several different word lists:
- Collins Scrabble Words (found here: http://norvig.com/ngrams/) - the offical world scabble list (excluding North America)
- GNU Collaborative International Dictionary of English (http://gcide.gnu.org.ua/)
- A list I generated myself by downloading the whole e-book catalog of Project Gutenberg (https://www.gutenberg.org/), which was around 70,000 books (there’s no kill like overkill)
Logic would suggest the world official scrabble list being the most suitable (the North American offical list perhaps even more so), but the other sources provided a nice exercise in data extraction anyway.
/// Returns an immutable array of words that are between min and max length
auto readDictionary(int min=3, int max=14) {
return File("sowpods.txt","r")
.byLine
.filter!(a => a.length >= min && a.length <= max)
.array
.assumeUnique;
}
// create word list, and associative array for fast lookup
immutable words = readDictionary;
immutable fastLookup = words.enumerate(0)
.map!(a => tuple(a.value,a.index))
.assocArray;
Actual Words
We need something to search for, so it’s time to populate our grid with letters, and to do that, we’ll use the trusty old keyboard input, where the user types in the letters of the Wordament grid, going left to right, top to bottom.
For example, the Wordament grid shown previously would be input as such:
riotelupprsusaso
These letters will be transformed into an arrary of letters:
[[r],[i],[o],[t],[e],[l],[u],[p],[p],[r],[s],[u],[s],[a],[s],[o]]
Each tile path becomes an index to the array, and forms a word. For example, the path [0,1,2,3] would generate the word “riot”.
Now you might ask “why an array of strings? why not just a single string, and index that directly?”. Well, it’s so we can account for the types of Wordament games where a tile may contain more than one letter.
Take this grid:

To input multi-letter tiles, we use a space as a delimiter, and would type as follows:
lnifserp ar ioefkel
This gets turned into the array:
[[l],[n],[i],[f],[s],[e],[r],[p],[ar],[i],[o],[e],[f],[k],[e],[l]]
Indexing remains the same; the path [1,5,8] would generate the word “near”.
auto getLetters(T) (T line) {
string[] letters;
letters.length=Grid.size;
auto index=0;
auto multiWord=false;
import std.ascii : toLower, isAlpha;
foreach (letter; line.filter!(a => a.isAlpha || a==' ')) { // only letters and space
if (index >= letters.length) throw new Exception ("Error: too many letters");
if (letter == ' '){
multiWord = !multiWord;
} else {
letters[index]~=letter.toLower;
}
if (!multiWord) index++;
}
if (letters.canFind!(a => a.empty)) throw new Exception ("Error: not enough letters");
return letters;
}
unittest {
assert ("qwertyuioplkjhgf".getLetters.equal(["q","w","e","r",
"t","y","u","i",
"o","p","l","k",
"j","h","g","f"]));
}
The Main Loop
Time to bring all the elements together:
- Get letter grid input from user
- Iterate through all possible paths
- For each path, map it against the grid, and create a word
- Check word against the dictionary, storing all words that are found
- Once all paths have been checked, print the results
void main(){
// timer code
import std.datetime.stopwatch;
auto sw = StopWatch();
immutable words = readDictionary;
immutable fastLookup = words.enumerate(0)
.map!(a => tuple(a.value,a.index))
.assocArray;
// enter input loop;
while (true) {
write ("Enter > ");
auto line = readln;
if (line.startsWith ("exit")) break;
try {
sw.start;
auto letters = line.getLetters;
alias Path = Tile[Grid.size];
Path currentPath = TileNA.repeat(Grid.size).array;
assert (currentPath.length == letters.length);
auto currentIndex=0; // keep track of where in the path we are
int[] foundWords;
void traverse (Tile tile) {
currentPath[currentIndex] = tile;
currentIndex++;
foreach (n; tile.neighbours) {
// don't step to a tile which is already in the path
if (!currentPath[].canFind(n)) traverse (n);
}
// finished path here
// construct a word from path
auto toTest = currentPath[].filter!(a => a!=TileNA)
.map!(a => letters[a])
.to!string;
// check if word in dictionary
auto wordIndex = fastLookup.get(toTest,-1);
if (wordIndex != -1) foundWords ~= wordIndex;
currentIndex--;
currentPath[currentIndex] = TileNA;
}
iota(0,Grid.size).each!(a => traverse(a));
sw.stop;
auto timeTaken = sw.peek.split;
// finished search, pretty print results
import std.string : leftJustify;
auto uniqueFound = foundWords.sort.uniq;
writefln ("Total words found: %s, time taken %s s, %s ms",
uniqueFound.count,
timeTaken.seconds,
timeTaken.msecs);
uniqueFound
.map!(a => words[a].dup)
.array
// sort by length, then by alphabet
.multiSort!((a,b) => a.length > b.length, (a,b) => a < b)
// print in 5 columns
.map!(a => a.to!string.leftJustify(16,' '))
.chunks(5)
.map!(a => a.joiner(" "))
.each!(a => a.writeln);
} catch (Exception ex) {
ex.msg.writeln;
}
}
return;
}
Game Time
Warm up finger exercises? Check.
Sports drink to the ready? Check.
Enthusiastic crowd of supporters? Check.
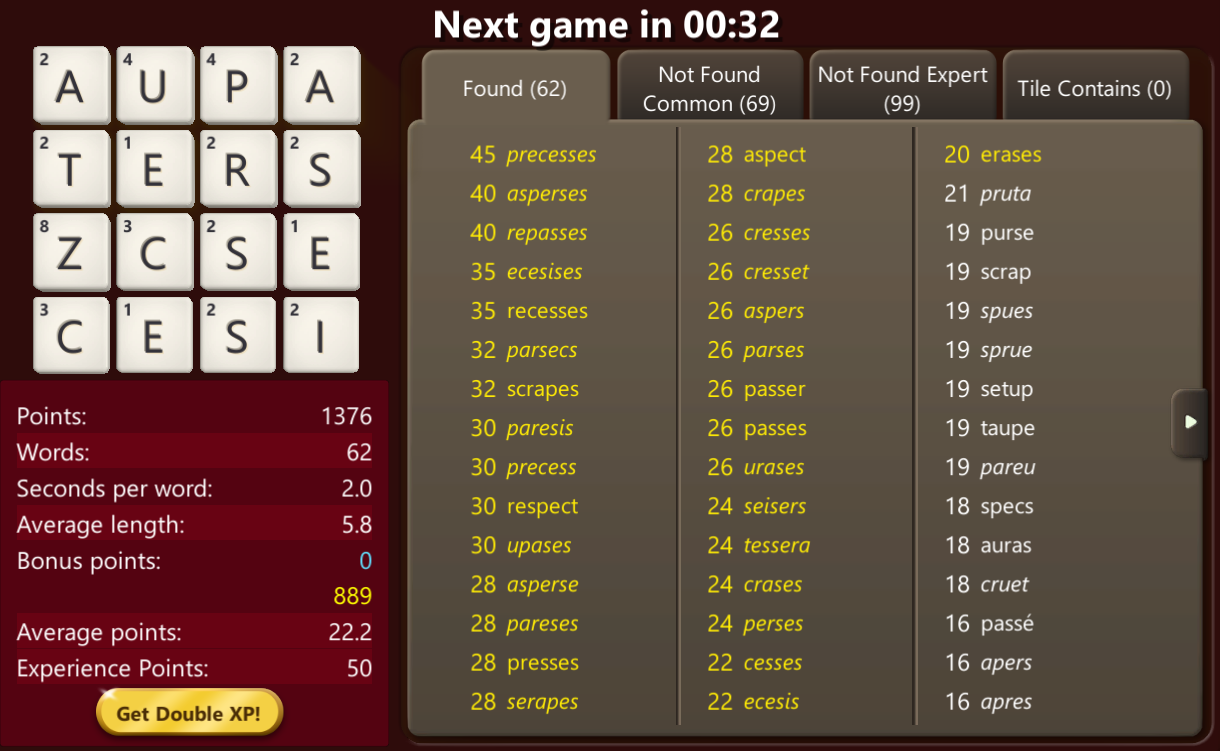
Loading up Wordament on my PC, the following grid appeared:

I enter the line into my solver:
Enter > aupaterszcsecesi
A hush falls upon the crowd, as the solver searches for words, the seconds ticking by…
After what seems like an eternity, the words are displayed:
Enter > aupaterszcsecesi
Total words found: 220, time taken 5 s, 96 ms
precesses asperses ecesises recesses repasses
asperse cresses cresset pareses paresis
parsecs precess presses respect scrapes
seisers serapes tessera aspect aspers
cesses crapes crases ecesis erases
parsec parses passer passes perses
prases preset prezes purses putzes
recces recess repass reseat reseau
resect scrape scraps secret seiser
seises sepses serape setups spares
sparse sprues taupes terces upases
urases apers apres apses arses
arsis asper asses asset auras
aurei aures ceres crape craps
crass cress cruet erase erect
erses esses pares pareu parse
pases passe peres perse prase
presa prese press pruta purse
rapes rases recce recta reset
scrap seise seres setup sises
spare spars specs sprue spues
spurs sputa taupe tepas terce
terse turps urase aper apes
apse arcs area ares arse
ates aura ceps cere cess
crap ecru eras eses pare
pars pase pass peat pecs
pere prez pure purs putz
rape raps rase rasp recs
reis reps rues seat secs
sect seis sera sere sers
seta spar spec spue spur
tepa tups upas urea urps
ursa utes zeps zeta ape
arc are ars asp ass
ate cep cru eat eau
era ere ers ess eta
par pas pea pec per
pes pet pur put rap
ras rec rei rep res
ret rue rut sap sea
sec sei ser set sis
spa tae tau tea tup
ups urp uta ute zep
I go back to the game, take a deep breath, and simply start typing the words as fast as I can. The crowd starts cheering, amazed at the skill on display before them - precesses…BANG - 45 points, asperses…BOOM - 40 points…the crowd goes wild, all thinking the same thing: can this Wordament warrior improve on his usual 200-300 odd point scores?
Funnily enough, yes, as it turns out, I can:
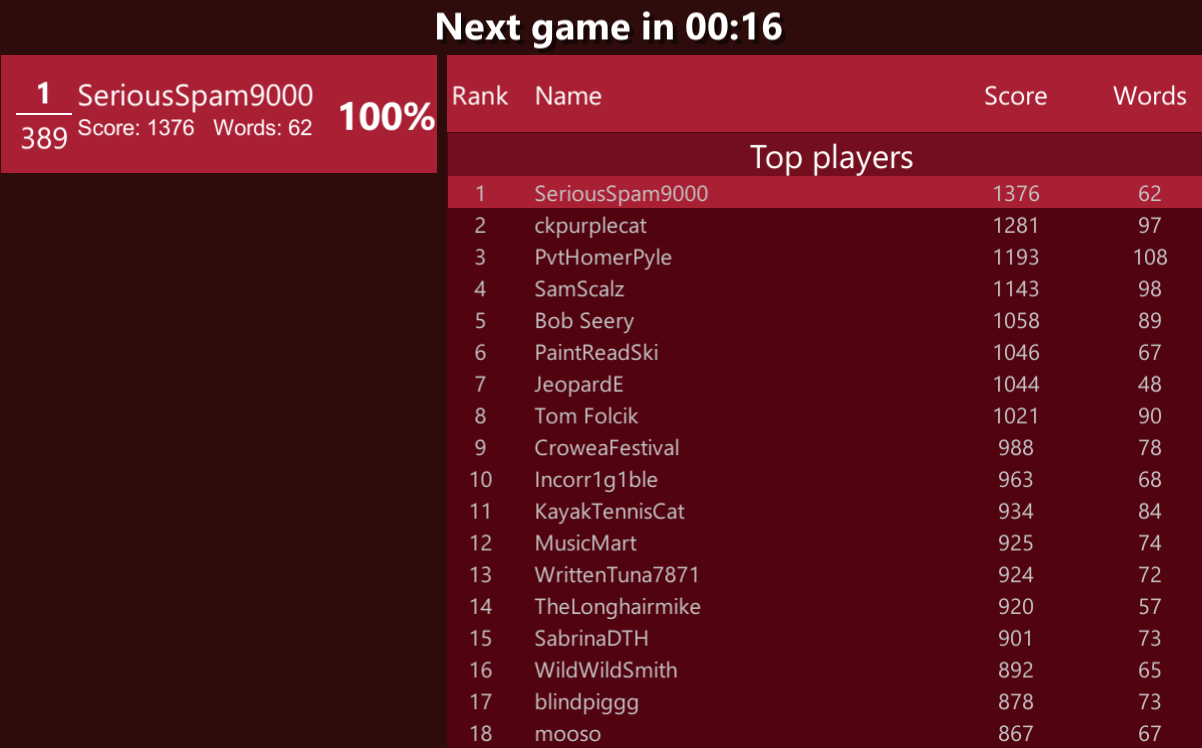
Victory! The crowd erupts! My dedication and hard work learning new words and patterns and putting in the hours of practice has paid off!
Ok maybe not quite that, but to be fair, it did take me a good weekend creating this solver (plus the extra hours spent sidetracked by making my own word frequency lists). The solver was an enjoyable exercise, but there are a few things that could be worked upon:
- Online solvers seem to take less than a second (my solver ~5 seconds). This peeves me; I think Path iteration can most likely be done in parallel, which should result in a 2-3x speed improvement
- Instead of manually typing in the results, investigate the solver automatically typing in the input. Less excitment for the crowd, but hey, all that typing takes its toll on the body
- The results of the word search is ordered by word length, but may be better to order by word score
- The additional modes that Wordament offers (such as tiles with an either/or letter, or words that end with certain letters, or even just a high value letter) are still to be implemented
These things could well become a future blog post, but until then, I shall take a break from Wordament, as I expect to be asked to do an interview with ESPN any moment now…


Share this post
Twitter
Google+
Facebook
Reddit
LinkedIn
Email